Welcome to my Master’s thesis. This webpage provides supporting information for my project, in particular, animations that could not be depicted in the report for the various models. I hope you enjoy them.
For those who have stumbled upon this, a “quick” read of my Master’s thesis may be of interest.
A 2D Kinetic Theory of Gases Model was developed in Python, in particular, using the Mesa agent-based modelling package. Some results of this model were visualized and can be seen below:
2D Gas model animation with energy distribution
The below animation was created using matplotlib.
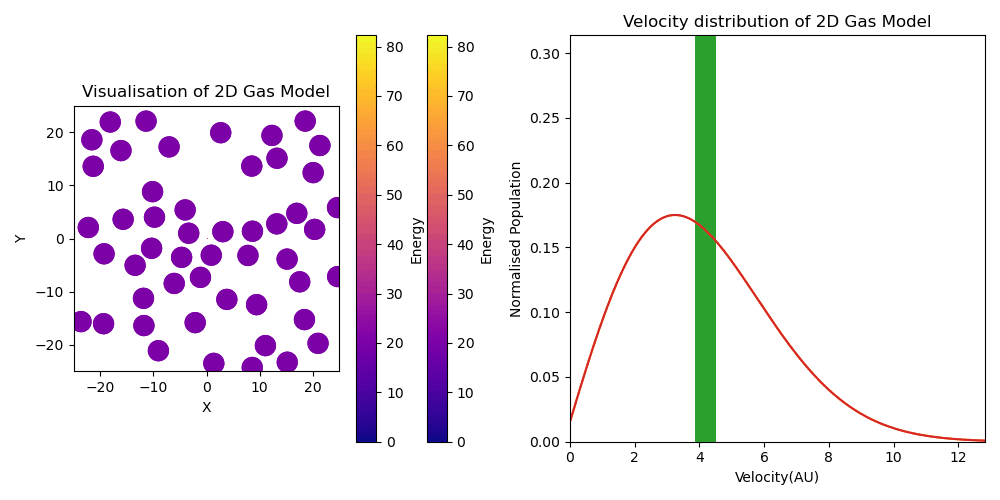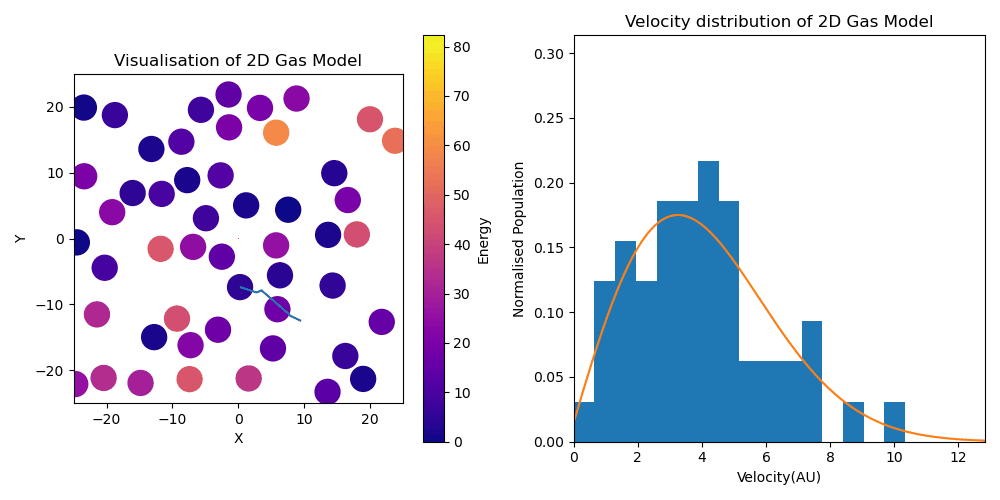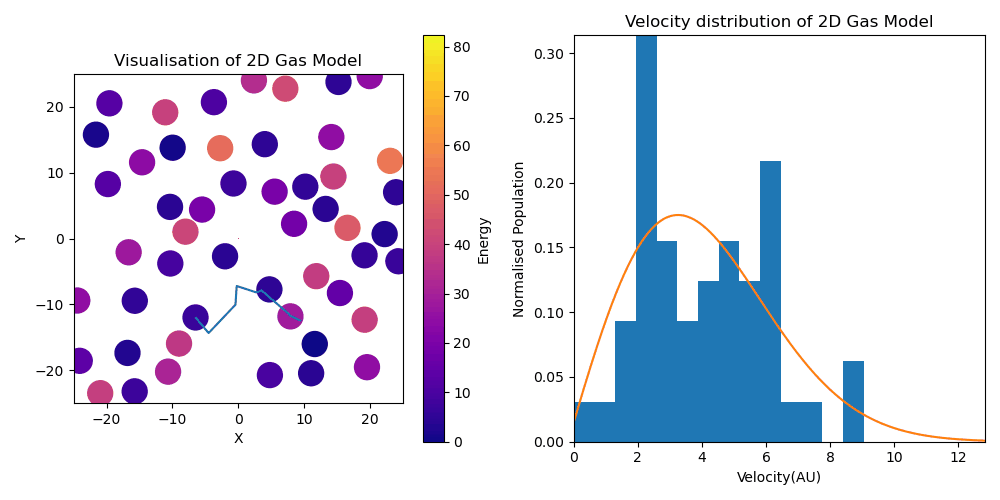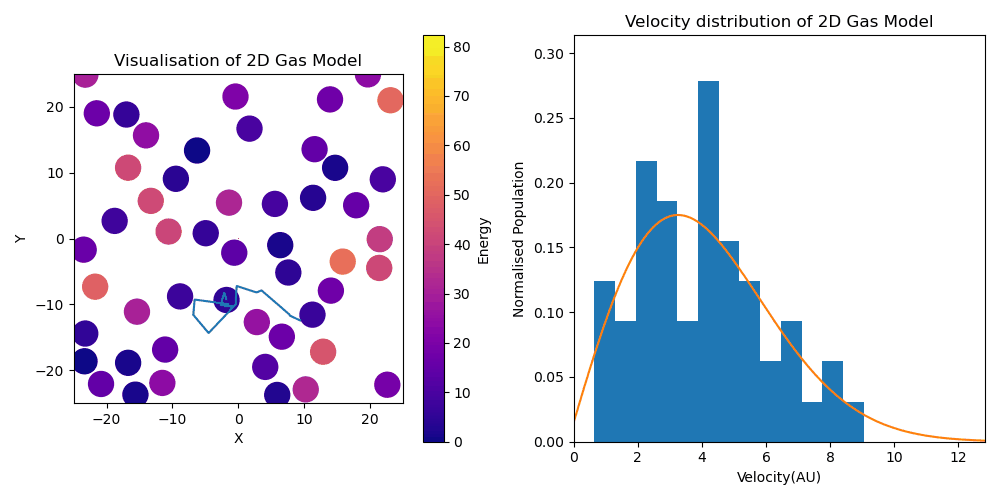
(LHS) Animation visualizing movement of particles within 2D Kinetic Theory of Gases Model. Particles have color based on their energies. (RHS) Parallel visualization of velocity distribution of particles synchronized to the visualization in the LHS. Depicts relaxation from initially equal velocity of all agents to a Maxwell-Boltzmann distribution, indicated by the distribution in orange. Note that the MB distribution was fitted to an averaged final velocity distribution.
Understanding 2D Collision dynamics
The 2D collision dynamics of this model are explained in the below diagram. The key aspect being rotating the frame of reference to separate the independent components of the velocities of the particles from the components involved in the collision. For further details, consult the thesis:
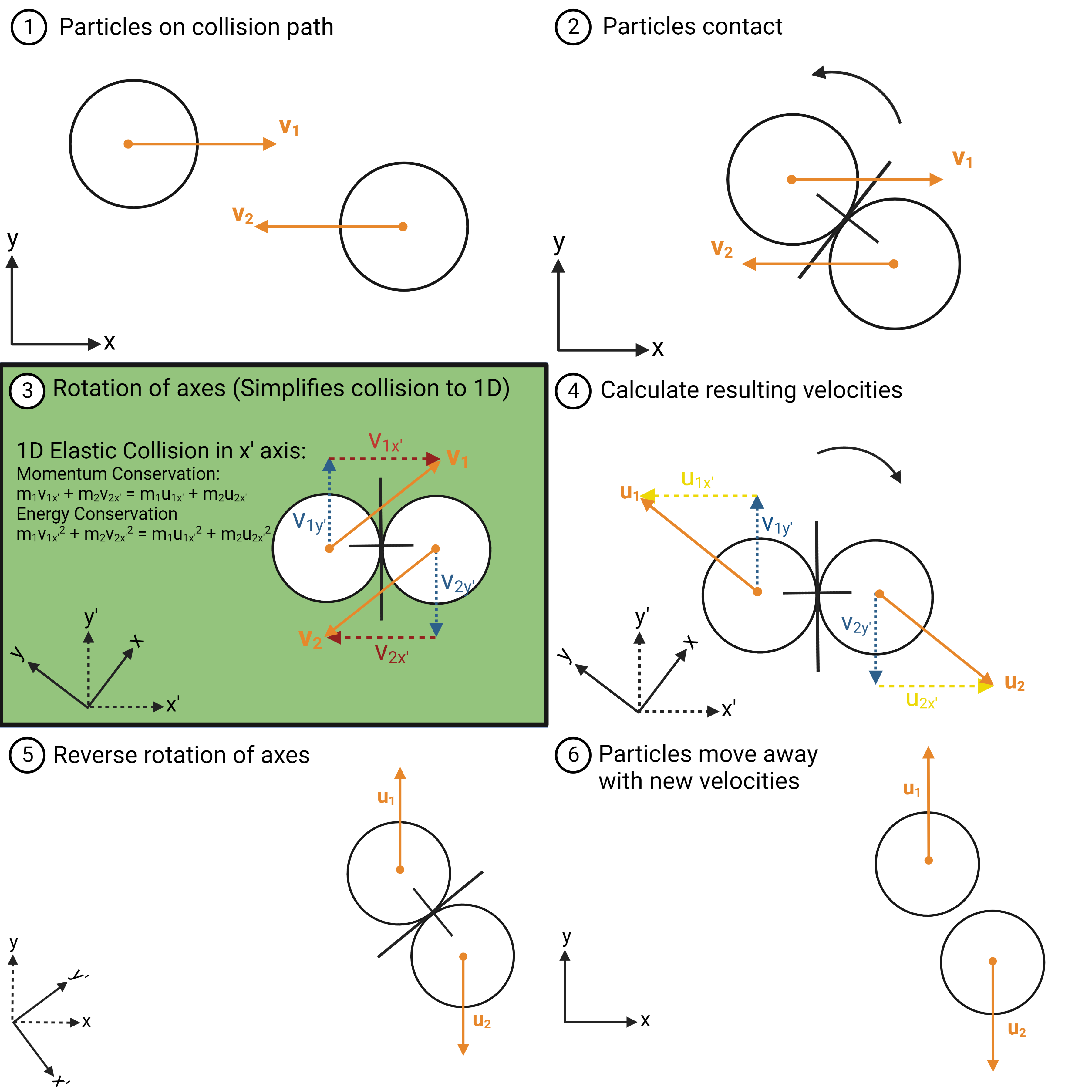
A Pseudo-2D Kinetic Theory of Gases Model was developed as an adaptation of the 2D Gas Model, removing its geometric dependence (positions of particles), while attempting to retain the reality of the kinetic theory model.
Velocity distribution of a Pseudo 2D Model
The resulting velocity distribution from this model is depicted in the diagram below.
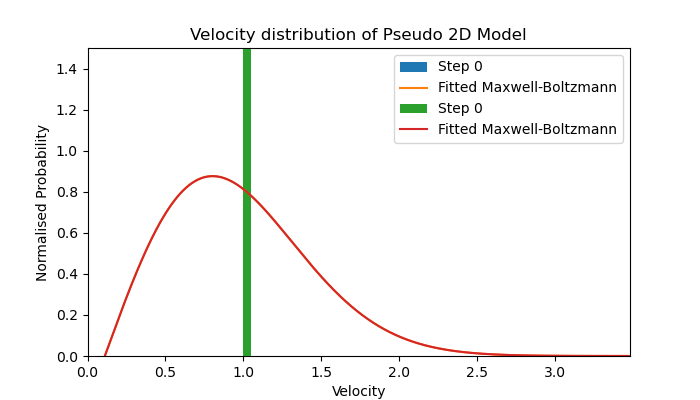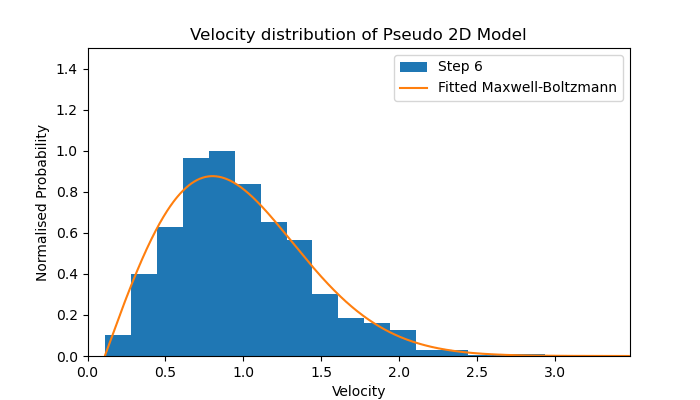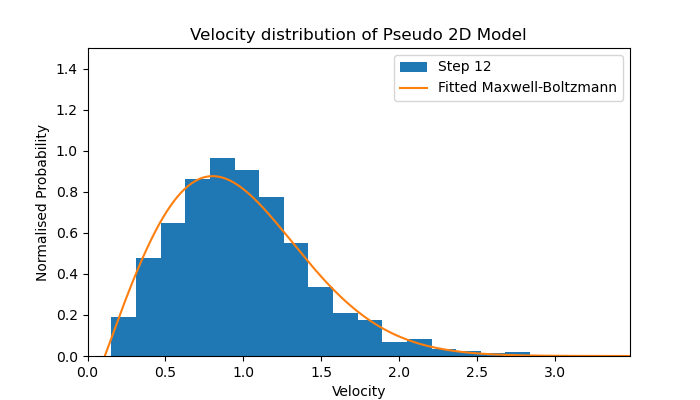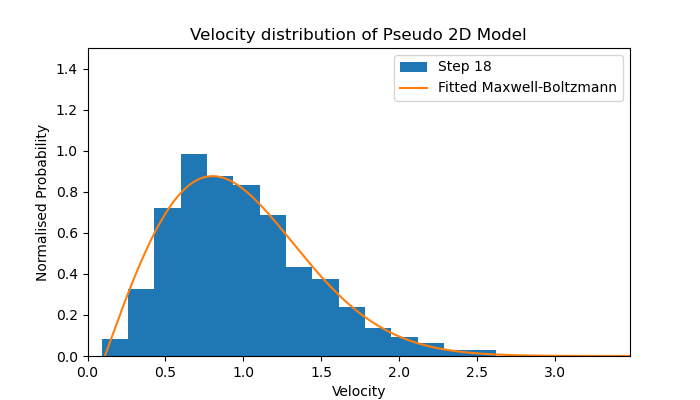
The animation clearly shows an instant relaxation from all individuals having identical velocity to forming the shape of the fitted Maxwell-Boltzmann distribution (fitted to an average of the final 10 distributions).
Energy distribution of a Homogeneous Saving Parameter simulation
Later, the model incorporated a saving parameter to emulate saving in economic systems. This essentially allows individuals to save a proportion of their energy/wealth from involvement in a transaction. The animation depicted below is of a simulation in which all agents have the same saving parameter (homogeneous) of 0.5. The consequence of this parameter is that the exponential Maxwell-Boltzmann distribution in energy/money is shifted higher, becoming a peaked energy/money distribution with exponential decay on either side, resembling a Maxwell-Boltzmann distribution in velocity. Evolution of this energy/money distribution is seen in the animation below.
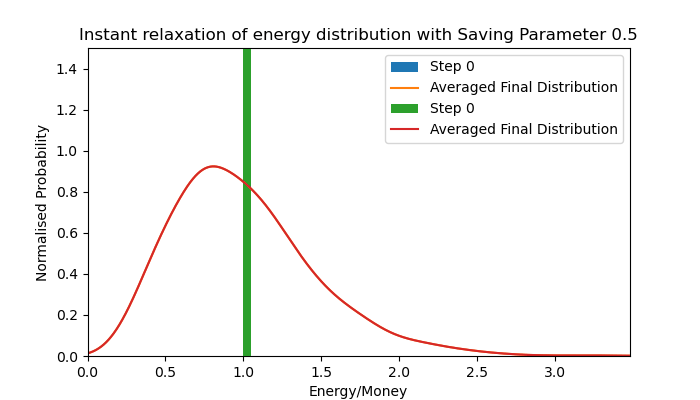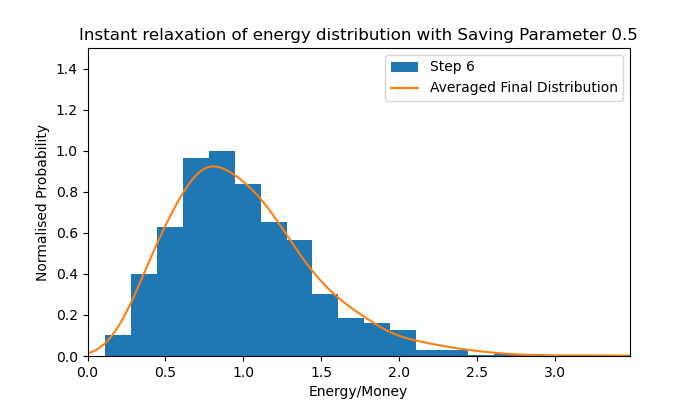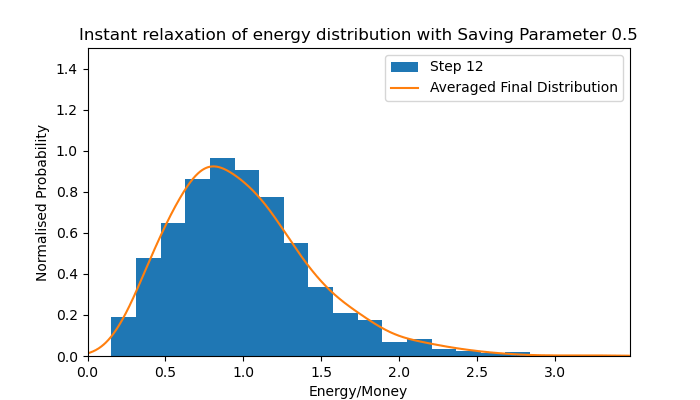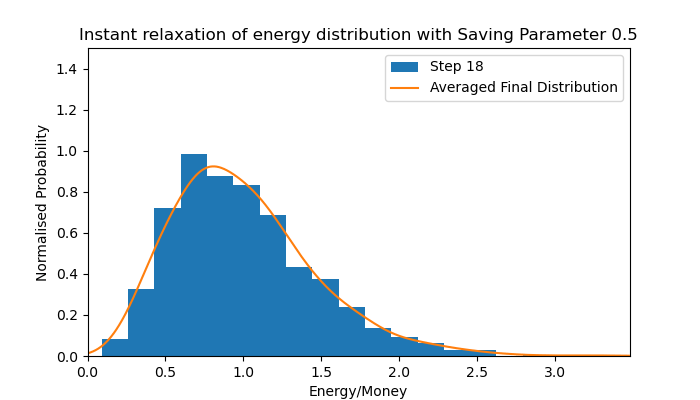
The animation shows an instant relaxation from all individuals having equal energy/money to forming the Maxwell-Boltzmann-like distribution of the averaged final distribution for a simulation with a homogeneous saving parameter of 0.5. The proposed effect of this saving parameter is to limit the amount of energy/money risked by all parties in an interaction, reducing the average amount gained and lost, thus contracting the peak. This effect is more clear in the results of the thesis.